An Overview of Multiferroics
Topics on this page:
Below we'll get into some more detail about multiferroics. If you already known enough about the subject you can browse through our nuggets page to see our results. In short, we aim to understand the dynamical magnetoelectric coupling between dielectric and magnetic orders. A few questions we can address are:
- Is the interaction between magnetic and electric orders direct, or does the lattice play a mingling role?
- Is the electromagnon the cause of the magnetoelectric coupling, or rather its signature?
- What are the fundamental excitations behind the formation of the ferroelectric polarization?
- Are the couplings between dynamical (phonons and magnons) and static (polarization and magnetization) the same?
Introduction
Generally speaking, multiferroics are materials that show two simultaneous ferroic (electric, magnetic and elastic) orders. However, the recent buzz about multiferroics concerns particularly materials showing a coexistence of dielectric and magnetic ordering. These sub-set of "magnetoelectric multiferroics" potentially have a variety of applications in spintronics and hybrid memory.
Multiferroics also open a series of questions concerning the fundamental excitations undelying their physical behavior. These are the topics that we work on.
The first ideas
 The idea of materials having simultaneous dielectric and magnetic
order are not new. Indeed, in 1984 ESPCI scientist Pierre Curie wrote
an extensive paper [P. Curie, J. Phys. (Paris) Colloq. 3, 393
(1984)] discussing the symmetry constraints
required for a material to react to both electric and magnetic fields.
The idea of materials having simultaneous dielectric and magnetic
order are not new. Indeed, in 1984 ESPCI scientist Pierre Curie wrote
an extensive paper [P. Curie, J. Phys. (Paris) Colloq. 3, 393
(1984)] discussing the symmetry constraints
required for a material to react to both electric and magnetic fields.
Landau mentioned this problem briefly to this problem in the late 50's [L.D. Landau and E.M. Lifshitz, Electrodynamics of continuous me dia (1959)] but dismissed it under the pretext that " it seems that till present, presumably, they have not been observed in any substance."
Landau missed this coach by little. The first magnetoelectric multiferroics date from the 60's [E. Ascher, H. Rieder. H. Schmid, & H. Sössel, J. Appl. Phys. 37, 1404 (1966)]. But the field remained dormant until 1994 when Hans Schmid coined the term Multiferroics:
[...] materials, in which two or all three of the properties 'ferroelectricity' 'ferromagnetism' and 'ferroelasticity' occur simultaneously in the same phase, and in which the magnetic point group has been reliably established by magnetoelectric, optical, dielectric, magnetic and related studies on single crystals and single domains.
Hans Schmid, Ferroelectrics 162, 317-338 (1994).
The real boom in multifeeroics had to wait a few more years for the discovery of magnetic field control of the electric polarization in TbMnO3 [T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima, & Y. Tokura, Nature, 426, 55 (2003)] and the large polarization in BiFeO3 thin films [J. Wang et al., 299, 1719 (2003)].
Better understanding the meaning of multiferroicity
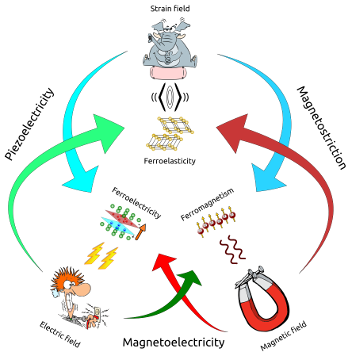
The Multiferroics Totem (figure to the right) can help us better understand the interest of these materials. Although more exotic p have been proposed, there are three well established and understood ferroic orders: ferroelasticity, ferroelectricity and ferromagnetism.
A ferroic order implies that a crystalline material has a spontaneous long range alignement of some microscopic property, leading to a macroscopic spontaneous property, named the order parameter. A necessary property of ferroic materials is that a suitable external field is able to switch the direction of the order parameter. Another important characteristic of ferroic materials is the existence of the spontaneous macroscopic property in the absence of any external field.
In Ferroelastic materials the microscopic property is the unit cell deformation and the macroscopic property is called strain. An external stress field can modify the strain (and deformation) direction. All (almost) ferroelectric materials are also ferroelastic and hence, per definition, multiferroic. NiTi alloys, also known as nitinol, is ferroelastic but not ferroelectric.
In Ferroelectrics, the splitting of the barycenter of the positive and negative charges in a unit cell create a microscopic electrical dipole momentum, which in turn produce a macroscopic electrical polarization. An external electric field can alter the polarization (and dipole) direction. BaTiO3 is one of the most knwon ferroelectric materials.
Electronic spins (generally) carry the microscopic magnetic moment in Ferromagnets and produce a macroscopic magnetization that can be switched by a magnetic field. Plain vanilla iron is ferromagnetic below 1040 K.
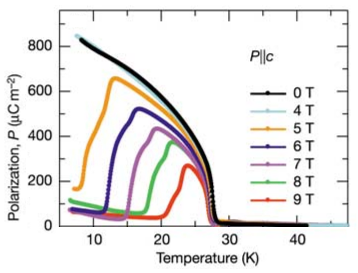
Each field acts on its associated order parameter. But a crossed action is even more interesting. The most well known crossed action is piezoelectricity which couples ferroelectricity and ferroelasticity. Here an electric field can produce a macroscopic strain and an external stress can act upon the polarization. One can thus use piezoelectricity to obtain accurate positioning using electric fields or getting a voltage drop by applying stress.
Magnetostriction is the crossed action between ferroelasticity and ferromagnetism. But the crossed action that is getting all the hype nowadays is magnetoelectricity.
Magnetoelectric Multiferroics (or simply multiferroics or even M&Ms) have the property of allowing to control electrical properties with a magnetic field and magnetic properties with an electric field. This is beautifully illustrated by Kimura et al. data shown above. Below 27 K, TbMnO3, an orthorhombic material, is both antiferromagnetic (What??? -- see "Types of Multiferroics") and ferroelectric. Its electrical polarisation lies along the c axis. Applying a magnetic field along the b axis will make the electrical polarization vanish from the c direction (and eventually appear along a).
Go back to "Multiferroics Home"
Proceed to "Types of Multiferroics"
