Types of Multiferroics
Topics on this page:
Antiferromagnets are welcome
One of the major problems in (magnetoelectric) multiferroics, is that we do not know many of them. In a milestone paper Nicola (then Hill) Spaldin [N. Hill J. Phys. Chem. B 104, 6694 (2000)] raised three main reasons why there are so few M&Ms:
1. Symmetry considerations
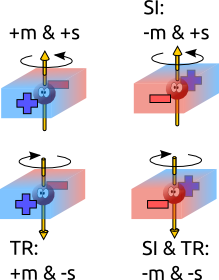
In a multiferroic the presence of an electrical dipole in the unit cell implies that the spatial inversion symmetry is broken. To understand this just remember that an electrical dipole comes from a splitting in the barycenter of positive and negative charges in the unit cell. In other words, one side of the cell is different from the opposite side. This cannot happen if the cell is centro-symmetric. Therefore, if one applies a spatial inversion operator to the cell, positive and negative barycenters will change places and the electrical polarization reverses. Spatial inversion symmetry breaking is a necessary condition for ferroelectricity.
But how about spins? Magnetic moments can be imagined as a charge in a closed orbit. This is a pseudovector and is therefore immune to changes produced by a spatial inversion operation. However, in order to have a well defined magnetic orientation the material must have loose a symmetry operation that keeps the spin unchanged in the disordered phase and reverses it in the ordered phase. This operation is time reversal. In the above analogy, time reversal would make the charge move in the opposite direction and hence switch the magnetic moment. When time reversal symmetry is preserved, the total magnetic moment is unchanged. When it is broken, then you have switchable magnetic ordering.
Time reversal symmetry breaking, however, do not act on polar vectors such as the electrical dipole. Hence, in order to be a multiferroic, a material must break both spatial inversion and time reversal symmetries.
The fist Spaldin's argument is statistical. There are 122 Shubnikov's magnetic symmetry point groups. Out of these, only 13 allow for both polarization and magnetization to exist. However, the only value of this argument is to highligh the importance of symmetry. Nothing tells us that materials are equally distributed throughout Shubnikov's groups. Therefore, the reduction of the number of available groups does not tell us anything about the actual number of materials that can have both symmetry breakings.
So let's move on...
2. Ferromagnets like to be metallic
This is a more serious argument. Many ferromagnets are elemental (Fe, Ni, Co, Gd, Dy) and alloys of them. These materials have partially filled d shells which in absence of particular orbital hybridization lead to high density of states at the Fermi level. In a ferroelectric material, there is a voltage drop due to the electrical dipole. If the material is metallic, this voltage creates a charge flow that will set the drop to zero. Hence, ferroelectrics need an insulating medium. An important note to the future: antiferromagnets (including those with canted weak ferromagnetism) are quite often insulating...
3. d electrons inhibit perovskite distortions
The reasons are not clear why, but distortions that lead to ferroelectricity in perovskites seem to be inhibited as soon as d shells, necessary for magnetism, begin to fill. In her paper, Spaldin especulates over a few possible reasons such as ionic sizes, dominant non ferroelectric distortions (Jahn-Teller for exemple), and/or electronic structure effects. None of these possibilities seem to dominate over the others. And there is no obvious sign that they are even important. But, at the end of the day, the distortion is still not there.
And so bothered we are. Only a handful of materials (BiFeO3, YMnO3, and a few others) are simultaneously ferromagnetic and ferroelectric.
But everything is not lost. Many of the hampering conditions for inhibiting ferroelectricity in ferromagnets are not present in anti-ferromagnets. In particular metallicity is often absent. We are still short of a wealth of multiferroics but the prognosis is way more positive. We have a few dozens of multiferroics if we accept antiferromagnts in the club.
And always look at the bright side of life. In an antiferromagnet, all we need to get a ferromagnetic momentum is a little spin canting. And all the applications would be available.
And then you like it!
Type I Multiferroics
Once we accepted antiferroics in the club, we end up with a large number of materials. As soon as this happens we have the urge for taxonomy. Daniel Khomskii [Physics 2, 20 (2009)] took care of this classification. He subdived multiferroics in two classes.
Type I multiferroics are regular ferroelectrics which happen to be also (anti)ferromagnetic. Let's briefly look at a few properties of BiFeO3, the leading type I multiferroic.
Temperatures / Size of polarization / Coupling constantsType II Multiferroics
Type II multiferroics, from the perspective of fundamental physics, are more exciting. In these materials, one of the orders (generally ferroelectricity) is a consequence of the other (generally antiferromagnetism).
Temperatures / Size of polarization / Coupling constants / Comparative table BiFeO3 TbMnO3Go back to "Multiferroics Overview"
Proceed to "Lattice Dynamics"
